Geometri ve hesap.. hesab ve hendese.. bizde doğuştan bulunan önsel ve yaratılıştan verilen kabli ilkelere ve mebdelere dayanır.. biz bunun bize emanet olarak verilen ayniyet (özdeşlik, identity) mebdesine dayandığını düşünüyorum.


Bir insan matemetik, geometri ve aritmetik eğitimi almasa bile yaratılıştan sahib olduğu bir mantığa göre düşünür ve buna göre oluşan nutuk ve dile sahib olur.. dünyevi sorumluluk ve uhrevi yükümlülük için bir emanete daha ihtiyaç var o da özgürlük ve hürriyettir. Bu ikisi ile bilim ve hukuku kurup geliştirebilir.. zaten dilin olmazsa olmaz iki koşulu olan dil ve din.. dahi insana bunun için bindirilmiş ve indirilmiştir.


Aristo ile iki bin yıl önce ORGANAN ile suri (şekli) mantığın esası olan kutbi değerler, sonra uygulamaya dönük nisbi değerler kümesi olan "0" değerli aritmetik, daha önce saptanmış olan geometri ile ortaya BİLİM dili çıktı.


Bu gün geldiğimiz aşama, bu ana karadan ilk ayrılın günlük dilin üzerine bilimsel bilgi, felsefi bilgi ve dini bilgi katmanları ayrıldı. Yukarıda bilim ve onun dili olan matematikten bahsettik.. bu kesin ve net dil.. çok yönlü ve yanlı konuları, alanları ve katmanları "söz" konusu eden felsefe ve din alanında fazla bir yarar sağlamıyor. Günlük dilin düz yazısının muğlak bulutundan sıyrılmak gerekiyor. Biz YBA ile bunu sağlamaya aday bir yöntem ortaya koyduğumuza inanıyoruz.. belki sanıyorum demek gerekirken ve var sayı ve sanı.. öngörme ve kestirme.. umuyorum ve bekliyorum.. aşamalarını da geçerek "inanıyorum" dememi pencereme bağışlayın.. çünkü düşünürken.. kurulan örgüyü, bilinen örtüyü, anlaşılan perdeyi ve açılan penceri.. pek göz önüne almayız.


İşte YBA bize bunu fark ettiriyor! Yetmez mi ?


KARARLI DENGE


Geometrik.. anlatım
aritmetik.. anlatım
matematik.. anlatım
bilimin dili ve deduksiyonu ve bir tur topografyası..


faraziye.. varsayımı
nazariye.. öngörümü
kanun anlamı
ise bilimin dini ve hipotetigi ve bir tur ütopyası


Bu topografya ve ütopya ile BİLİMCİLER nihai bir kuram peşinde koşarlar ve bununla da sicim kuramiyle buluşmuş sanıyorlar.. yaklaşıyoruz deselerde daha BİLİMSEL olabileceklerdi…


Bu sabah biz onların ayağını bir “yumurta” ve “zeytin” ile yere değdirdik...



İşbu alıntı yazıyı okuduğunuzda geometri tarihimizi bilmiş olacaksınız. Oklid ve oklid dışı geometrilerin ögrenilmesi .. bilimci kesin bilgi safsatasi ve dincilerin kuşkusuz inanç saltanati ile insan zihnine sağladıği kolayliklarla bereber miskin şuurları bloke ederek kulturumuze saldigi hakimiyetim kaldirilmasina vesile oldu.


Felsefe ve din arasinda.. hızlı anlam sürücüsü ve kolay anlatim aygiti ile.. ortak bir platform oluşturacak YBA (Yöntem Bilimsel Analiz) ile kuram ve deneyim arasinda konulan TAHTAREVALLİ.. ne zihni yumurta üzerindeki zeytin çekirdeği gibi tedirgin eder.. ne de yumurta kabuğunun içine oturmuş zeytin tanesi gibi donuk ve durgun bırakır.

Soru ve yanit ile sav ve kanit arama ve bulma surecinde sabit hak ile mutebeddil hakikat arasinda, kararlı ve kararsız denge uçlarıyla, binlerce yildir cereyan eden kavgayı YBA ortaya koyacağı yeni PARADİGMA kaldırılacaktır.

Bilimsel paradigmalar ve dini dogmalarin birbirini etkilimesiyle ortaya çikan öykünün de yararli ve verimli bir oyun oldugunun anlaşilmasiyla dilin bilim kanaliyle hikmete yöneldigi.. dinin hukuk kanaliyla ahlaka yol aldigi iyice anlasılacaktir.

Dilin ve dinin.. emegin ve özgurlugun.. çevrenin ve barisin insanlarin ortak degeri oldugunun anlasılmasiyla bunlarin partilere paravana ve alet.. ideolojilere paratoner ve bayrak.. yapilmasi olasiligi kalmayacaktir. çünkü artık ekonomik ve politik çıkar temin etmek için böylesine yağlı bir kaymak bulamayacaklardır. Herkesin haysiyeti (onuru) hasılatı ile bu hasılat (ürün) ancak proje ve ekip çalışmasıyla elde edilecek mal ve hizmet sunma, fazilet ve kemalat serme, başarısı kadar olacaktır.

Yaklaşık 30 yıl önce bir teknik olarak başlayan ve sonra yöntem haline gelen YONTEM BILIMSEL ANALIZ 2020 yılinda ete kemiğe bürünüp barindirdigi anlam surucusu ve anlatim aygiti ile dedüksiyonla örülen bezi ve hipotezle örtülen testi yoluyla gerçeğe dokunmak ve görmekten.. gerçeği dokumaya ve örmege geçen bir dil olmuştur.

Artik bundan sonra ilmek ilmek dokudgumuz DÜŞ çoraplarini basımıza geçirmek icab eder mi ?

Lif lif ördüğümüz DİL sepetlerini kafamiza koymamiza luzum var mı ?

Çorabi ayagina giy.. sepeti elinde taşi.. rahat edersin


https://sites.google.com/site/hakanparlak/%C3%B6klidd%C4%B1%C5%9F%C4%B1geometriler?fbclid=IwAR2EWk8w4Npty_sgG0PyGRmuop-hLLgtDCztlcJn_i5CBNACuOjuuucir7s


Öklid Dışı Geometriler
(Bu yazı Us Atölyesi dergisinin 10. sayısında yayımlanmıştır.)
EUCLİDES PENCERESİNDEN DIŞARIYA BİR BAKIŞ: EUCLİDES -DIŞI GEOMETRİLER
            
     Euclides-Dışı Geometrileri açıklamadan önce kısaca Euclides geometrisini bir hatırlamakta yarar olduğunu düşünüyorum. Euclides geometrisi doğru, çember, paralel doğrular, açılar, benzer üçgenler, düzlemler ve benzeri konuları inceleyen ve mükemmelleştirilmiş halini çoğumuzun ortaöğretim boyunca okuduğu geometridir. Belki insan düşüncesine en yakın olduğundan, belki de ilk düşünülen ve ikibin yıl alternatifi bulunamayan, ( aslında bir tek alternatifinin bile olamayacağına inanılan ) bir geometri olduğundan dolayı hala da ortaöğretimin temel derslerinden birisidir Euclides geometrisi. Bu isimle anılmasının sebebi bu geometrinin temellerinin yaklaşık olarak M.Ö. 300 yıllarında İskenderiye de büyük matematikçi Euclides tarafından yazılan ve onüç ciltten oluşan ‘Elementler’ de sistematik olarak işlenmiş olmasıdır. Euclides ‘Elementler’ in başlangıç bölümünde temel ilkeleri oluşturan önermelerin bir listesini vermiştir. Bunlar üç gruptur: Tanımlar, Aksiyomlar ve Postulatlar. Nokta, doğru, düzlem … v.b nin tanımı verildikten sonra Aksiyomlar yani Genel doğrular sıralanmıştır. Bunlar;

1.     Aynı şeye eşit olan şeyler birbirine eşittir.
2.     Eşit olan şeylere eşit şeyler eklendiğinde sonuçlar eşit olur.
3.     Eşit olan şeylerden eşit şeyler çıkarıldığında kalanlar eşittir.
4.     Birbiriyle çakışan şeyler birbirine eşittir
5.     Bütün parçasından büyüktür.
şeklindedir. Bunlardan sonra da Postulatlar yani aksiyomlar gibi ispatsız kabul olunan ama doğruluklarına o zamanki anlayışa göre aksiyomlar kadar kesin gözle bakılmayan temel önermeler sıralanmıştır. Euclides ‘in postulatları şunlardır:

1.     Bir doğru herhangi bir noktadan başka bir noktaya çizilebilir.
2.     Bir doğru parçası doğrusal bir çizgi üzerinde sürekli uzatılabilir.
3.     Bir daireyi herhangi bir merkez ve uzaklıkla belirleyebiliriz.
4.     Tüm dik açılar birbirine eşittir.
5.     Başka iki doğruyu kesen bir doğru bu iki doğruyla aynı tarafta, toplamları iki dik açıdan küçük iç açılar meydana getirirse bu iki doğrunun uzantıları, açıların iki dik açıdan küçük olduğu tarafta kesişirler.
            İşte bizim yazımızın kahramanı da bu beşinci postulattır. Beşinci postulat ya da paralellik postulatı diye adlandırılan bu ifade ‘Verilen bir doğruya verilen bir noktadan birden fazla paralel doğru çizilemez’ ifadesiyle matematiksel açıdan eşdeğerdir. Matematik tarihinde belki de hiçbir önerme sonuçları bakımından paralellik postulatı kadar etkili olmamıştır. Bu postulat daha baştan kuşkuyla karşılanmış, yüzyıllar boyunca doyuruculuğu tartışma konusu olmuştur.
            
            Euclides’in paralellik postulatı bağımsız mıydı ya da diğer postulatlardan çıkarsanabilir miydi? Bu soru matematikçileri 2000 yıl boyunca uğraştırmıştır. Eski çağda Ptolemy orta çağda Nasıreddin Tusi, 18.yüzyılda da Lambert ve Legendre bunun cevabını bulmaya çalıştı. Tüm bu insanlar postulatı kanıtlamaya çalışmış bu çalışmalarda çok önemli sonuçlar bulmuş ancak asıl hedefleri hep sonuçsuz kalmıştır.
           
            Paralellik postulatının bağımsız bir postulat olduğunu yani seçilebilecek başka bir postulata dayanan yeni geometrilerin de mantıksal olarak olanaklı olabileceğini ilk kestiren Gauss’tur. O zaman tarihler yaklaşık 1817 yi gösteriyor olmalı. Bunu Gauss’un mektuplarından tahmin ediyoruz. Ne var ki Gauss ulaştığı sonuçları açıklama yoluna gitmez bu konudaki düşüncelerini hiçbir zaman yayımlamaz. Daha sonra 1823 de Macar matematikçi Janos Bolyai başka bir postulata dayanan bir geometri kuramının olanaklı olduğunu buldu. Onunda çalışmalarına son şeklini vermesi uzun sürünce, Euclides-dışı geometri düşüncesini ilk gerçekleştiren ve 2000 yıllık geleneğe meydan okuyup düşüncelerini yayımlayan rus matematikçi Nikolai Ivanovitch Lobachevsky olmuştur.

             Lobachevsky’nin oluşturduğu yeni geometride beşinci postulatın yerine şu postulat kullanılmıştır. ‘Bir düzlem üzerinde bulunan d doğrusuna, dışındaki A gibi bir noktadan d doğrusuyla kesişmeyen birden fazla doğru çizilebilir.’ Lobachevsky’nin ‘imgesel geometri’ dediği bu geometriye günümüzde ‘hiperbolik geometri’ denmektedir.
          
            Gauss’un, Bolyai’nin ve Lobachevsky’nin birbirinden bağımsız olarak Göttingen, Budapeşte ve Kazan’da ortaya attığı temelleri benzer olan yeni düşüncelerin 2000 yıllık bir kuluçka döneminden sonra aynı dönemde ortaya çıkışı dikkat çekicidir.
           
             Euclides-dışı Geometri adını ilk kullanan ise Gauss’tur. O zamanki yaygın Kantçı felsefe Euclides-dışı geometriyi ciddiye almayı reddettiği için otuz, kırk yıl boyunca matematiğin anlaşılması güç bir alanı olarak kalmıştır.
       
          Kant'a göre, geometrinin konusu uzay, temel özelliklerini aklımızın yapısına borçluydu; geometrik önermeler bu nedenle zorunlu doğrulardı. Başka bir deyişle, bir tek geometriye olanak vardı, o da Euclides geometrisiydi. Birçok matematikçinin önceleri görmezden geldiği ve yok saydığı Euclides-dışı geometrinin önemini ilk kavrayan Riemann’dır. Riemann’nın ortaya koyduğu manifoldlar kuramı Euclides-dışı geometriye izin veriyor ve Riemann geometrileri denilen birçok yeni geometri ortaya çıkarıyordu. 1868 yılında da İtalyan matematikçi Beltrami Euclides-dışı geometrilerin kendi içlerinde tutarlılığını ispatlayarak artık bu konuda kalan tüm tereddütleri ortadan kaldırmıştır. Böylece geometride Euclides’in egemenliği matematikte de mutlak doğruluk düşüncesi yıkılmış oluyordu. Doğruluğu zorunlu gibi düşünülen postulatların varsayımdan öte bir şey olmadığı, matematiksel doğrululuğun göreceli olduğu, bir teoremin doğruluğunun dayandığı aksiyom ve postulatların doğruluğuna bağlı olduğu görülmüştür. Başka geometrilerin belirlediği başka uzaylarında olduğu belki de yaşadığımız evrenin de bu uzaylardan birine uyduğu düşünceleri ortaya çıkmıştır.
            
              Yazdıklarıma son vermeden son vermeden şunu belirtmek isterim ki günümüz matematiğinin en önemli konularından biri olan Topoloji en genel geometri olarak diğer tüm geometrileri kapsar. Genellik bakımından topolojiden sonra projektif geometri gelir ve çeşitli özelleştirmelerle diğer geometrilere ( Hiperbolik geometri, küresel,eliptik geometri, ..) ulaşılır. Ve bu yazıda adı geçen kavram ve kişiler de başka, başka yazılara konu olabilecek kadar derin ve değerlidir. Farklı bir zamanda bu konularda yine buluşmak dileğiyle.   
                                                                                                                                  

Hakan PARLAK

kesin bilgi..
kuşkusuz inanç..
İnsanlar üzerinde dört çelişki saptanmıştır;




ÇOĞUNLUKLA mutlu olanlar erdemli değildir.. erdemli olanlar mutlu değildir...
Kantın bu tespitinden başka EKSERİYETLE kuvvetli olanlar haklı değildir, haklı olanlar kuvvetli değildir...
Birde Emile Boutrox'un saptamıs var; zorunlu olanlar olası değildir.. olası olanlar zorunlu değildir.. Bunu biz izafiyet ve kuantım çekişmesi olarak biliriz.
Dördüncüsü insanlar kesin hakikatı arar.. fakat bununla kuşkusuz inancı yitirir.. kuşkusuz inancı ararsa kesin hakikatı bulamaz. Sanırım bu da benim keşfim olabilir.. eğer doğruysa.. fakat siz hiç doğruyu ve gerçekle yan yana getirebildiniz mi ? Peki hiç iyi ile güzele bir arada tutabildiniz mi ?


Sanırım tutamazsınız.. şu örnekle anlayabilirsiniz: Hem kırk yıldır yaptığınız cima gibi yasal bir seksin iyiliğin sekinetini yakalayacaksınız.. hem delicesine bir cesaretle zina gibi yasadışı bir birleşmenin güzelliğini ve heyecanını yakalayacaksınız.. bu olası değil gibi görünüyor.


Ancak ben öyle düşünmüyorum.. tapılası karılar ve kulluk edilesi kocalar bunu kırk yıl sonra da olsa gerçekleştirebilirler.. Fakat bu sümsük ve sünepe müslümanların yapacağı bir iş değildir.. Hem meşru cimanın seksi ve iyiliği ve dinginliği olsun hem gayrı meşru seksin tazeliği ve canlılığı ve güzelliği bulunsun.. bu uçuk gibi görünen çift taraflılığı hiç ölmeyecekmiş gibi dünyaya ve yarın ölecekmiş gibi ahirete çalışan kimseler yapabilir.


Elbette bu sadece çoğalma yasasının tezahürü cinsellik ve tensellikte değil.. tüm dinsellik ve tinsellik buyruk ve değerlerinde de yaşamak ve yaşatmak mümkün.. yeter ki samimi ve ciddi bir insan.. safi ve halis bir islam olalım... amma siz hem kuşkusuz bilgi ve hem kesin inanç peşinde koşarsanız.. ne gücünüzdeki bilginin "tat"ına ne de gürünüzdeki inancın "tut"una varamazsınız.. biz işimizde işte gücü ve gürü.. deme de tatı ve tutu.. birleştirerek yapabiliriz.


Bilgi, saygı, sevgi ve sağlıcakla kalınız.
Osmanziya 03.03.2022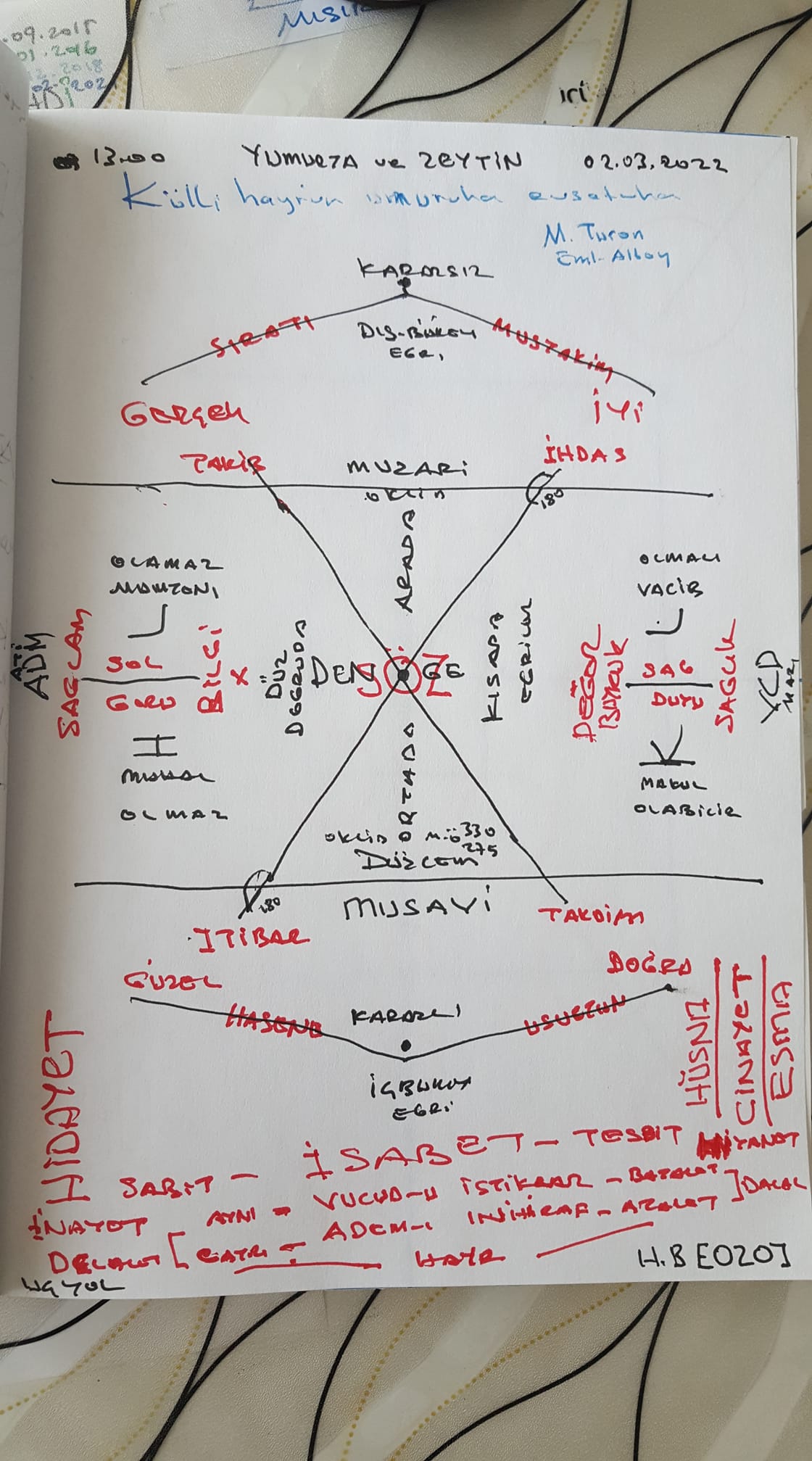







Düzenleyen osmanziya - 03-Mart-2022 Saat 06:17